← back to full list
Process

Given: 2,414 greyscale images of faces, each 48 x 42 pixels. Each pixel is represented by a number from 0 to 255, 0 black, 255 white. Using Principal Components Analysis, we can reduce the dimensionality of each image without much loss of detail.
I give mathematical background and derivations in this pdf.
"Eigenfaces"
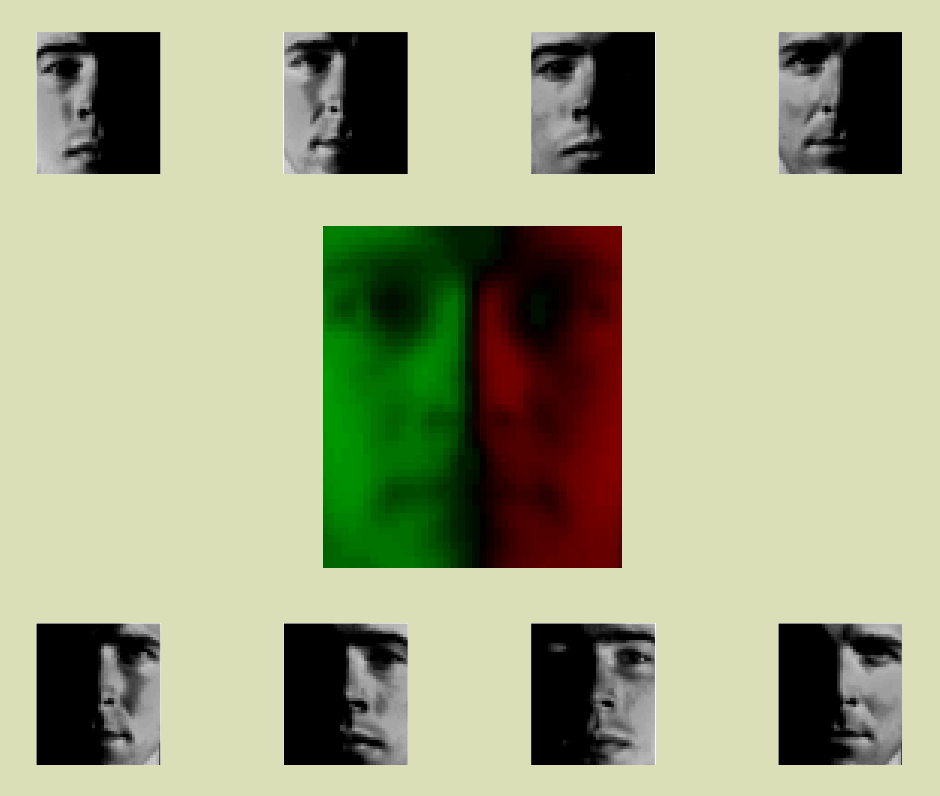
For the red and green "eigenface" below the following is true: the top row of faces are light where the eigenface is green, and dark where the eigenface is red. The reverse is true for the bottom row. The "eigenface" represents an eigenvector, which is an axis in many-dimensional space. Along this eigenvector, the faces above have positive coefficients, the faces below have negative coefficients. Click the arrow to cycle through the four principal eigenvectors, the axes along which there is the greatest variance in this data set.Results
By using the principal eigenvectors for our reduction, we can capture most of the variance in the data. In this case, only a small percentage of the original dimensions is needed.

Credits
The data set and direction of inquiry were provided by Gopal Nataraj, as adapted from an EECS 545 course at University of Michigan, taught by Professor Clayton Scott. The eigenface and results visualizations are my own.